
Digital lodging platform Airbnb Inc. (NASDAQ: ABNB) disappointed investors with its outlook for Q2 2023. The popular disruptor and innovator of BnB travel bookings have had gravity-defying growth and earnings throughout the weakening economy. It was a prime example of consumers shifting their discretionary spending towards services like Airbnb over goods like apparel. Airbnb is one of the major benefactors of the positive normalization of the travel and leisure industry in the post-pandemic era.
Other travel and leisure booking platforms, including Expedia Group Inc. (NASDAQ: EXPE), TripAdvisor (NASDAQ: TRIP), and Booking Holdings Inc. (NASDAQ: BKNG), have been benefactors in the travel recovery. The pent-up demand for leisure and vacation travel and lodging continues to drive spending even as other industries have been facing negative normalization after 2021 peaks.
Falling ADR Concerning
However, high inflation appears to be revealing some kinks in the armor for Airbnb as it lowered its forecasts for Q2 2023 revenues. The company insists that demand is still robust, and the lowered revenue range results from a more extensive mix and new Host pricing tools. However, the company expects average daily rates (ADR) to fall slightly.
This means there's pressure on margins from the inventory glut, causing landlords to lower their prices in the face of falling demand. Almost 80% of Airbnb rooms are going for under $100 per night, and its Airbnb Rooms, which are private rooms, are averaging $67 per night. This is good for customers but not for hosts or Airbnb’s top and bottom lines.
Strong Q1 2023 Earnings But Cautious
On May 9, 2023, Airbnb released its fiscal first-quarter 2023 results for March 2023. The company reported a GAAP earnings-per-share (EPS) profit of $0.18 versus consensus analyst estimates for a profit of $0.10, beating estimates by $0.08. Net income was $319 million for the quarter and $1.9 billion. Nights and Experiences Booked rose 19% YoY and 49% sequentially to 121 million.
While the U.S. saw stable growth in North American Nights and Experiences, Asia Pacific saw a 48% YoY spike as the region recovered from the pandemic. Revenues rose 20.5% year-over-year (YOY) to $1.82 billion, beating analyst estimates of $1.79 billion. Gross Bookings Value increased 19% YoY to $20.4 billion. The Average Daily Rate (ADR) was flat at $168 YoY. The company achieved GAAP profits again, which led them to raise its stock buyback program of up to $2.5 billion in stock or 3% of its market cap.
In-Line Guidance Fails to Impress
Airbnb issued in-line guidance for Q2 2023 with revenues of $2.35 billion to $2.45 billion versus $2.42 billion consensus analyst estimates. Nights and Experiences are expected to have unfavorable YoY comparisons, and growth is expected to be lower than revenue growth in the quarter. The company expects ADR to be slightly lower in Q2 2023 due to a mix of shifts and the launch of new Host pricing tools. Full-year 2023 adjusted EBITA margin is expected to be in line with the full-year 2022.
CEO Insights
IN THE CONFERENCE CALL, ABNB CEO Brian Chesky commented, "We have some big ideas for where to take Airbnb next. We're building the foundation for new products and services that we plan to launch in 2024 and beyond. At the same time, Airbnb is still underpenetrated in many markets around the world. So we're increasing our focus on these less mature markets, and we are already seeing positive results.” He noted that Germany and Brazil are two of its fastest-growing markets, credited with rolling out its expansion playbook for accelerated growth.
The company introduced Airbnb Rooms along with 50 new features and upgrades. They launched new pricing tools for Hosts enabling them to see what other Airbnbs in the area are charging along with listings in high demand and getting booked so that they can be more competitive. Longer stays past three months will get more discounts.
Airbnb rooms are the most affordable rate, with average prices of only $67 a night. He noted that 80% of Airbnb rooms are priced under $100. They also unveiled anti-party crackdowns to keep disruptive behavior down.
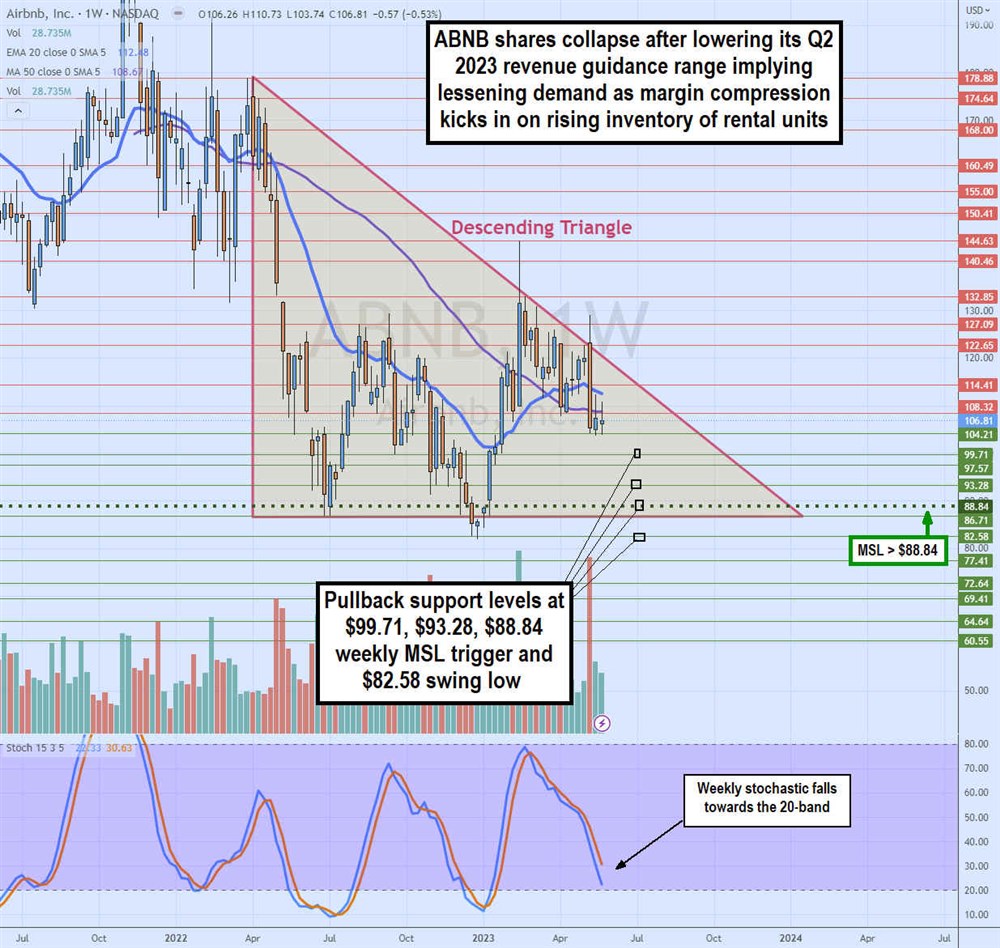
Weekly Descending Triangle
ABNB's weekly candlestick chart illustrates a descending triangle that commenced after peaking at $178.88 in April 2022. A descending triangle consists of a falling trendline indicating lower highs on bounces against a flat bottom trendline. ABNB formed a flat bottom of around $86.81 in December 2022. It triggered a weekly market structure low (MSL) breakout through $88.84 to stage a rally up to $144.63 in February 2023 before peaking at the triangle-falling trendline on consecutive breakout attempts.
The weekly stochastic peaked on its complete oscillation just under the 80-band before falling back towards the 20-band. The weekly 20-period exponential moving average (EMA) resistance is at $112.48, followed by the weekly 50-period MA at $108.67. Pullback support levels are at $99.71, $93.28, $88.84 weekly MSL trigger and $82.58 swing low.





